
Similarly for Neutrosophic Over-/Under-/Off-Logic, Probability, and Statistics Pons Publishing House: Brussels, Belgium, 2016 168p. Degree of Dependence and Independence of the (Sub)Components of Fuzzy Set and Neutrosophic Set. Standard Neutrosophic Soft Theory-Some First Results. Rough Standard Neutrosophic Sets: An Application on Standard Neutrosophic Information Systems. (I, T)-Standard neutrosophic rough set and its topologies properties. In Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, 10–12 September 2003 pp. Definition of neutrosophic logic-A generalization of the intuitionistic fuzzy logic. Neutrosophy: Neutrosophic Probability, Set, and Logic ProQuest Information & Learning: Ann Arbor, MI, USA, 1998 p.

Extended Nonstandard Neutrosophic Logic, Set, and Probability Based on Extended Nonstandard Analysis Cornell University: Ithaca, NY, USA, 2019 p.
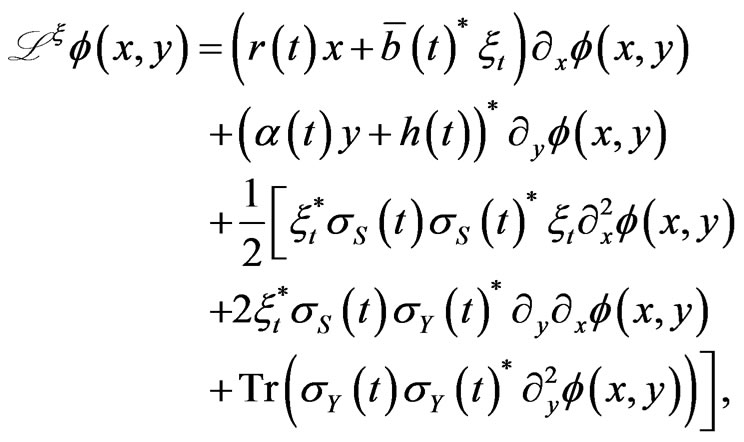
About Nonstandard Neutrosophic Logic (Answers to Imamura’s ‘Note on the Definition of Neutrosophic Logic’) Cornell University: New York City, NY, USA, 2019. Answers to Imamura Note on the Definition of Neutrosophic Logic.

Note on the Definition of Neutrosophic Logic. The author declares no conflict of interest. These were necessary in order to construct a general nonstandard neutrosophic real mobinad space, which is closed under the nonstandard neutrosophic arithmetic operations (such as addition, subtraction, multiplication, division, and power), which are needed in order to be able to define the nonstandard neutrosophic operators (such as conjunction, disjunction, negation, implication, and equivalence) on this space, and to transform the newly constructed nonstandard neutrosophic real mobinad space into a lattice of first order (as partially ordered nonstandard set, under the neutrosophic inequality ≤ N) and a lattice of second type (as algebraic structure, endowed with two binary laws: neutrosophic infimum ( infN) and neutrosophic supremum ( sup N)). That’s why we have extended in 1998 for the first time the monads to pierced binad, and then in 2019 for the second time we extended the left monad to left monad closed to the right, the right monad to right monad closed to the left, and the pierced binad to unpierced binad. Keywords: nonstandard analysis extended nonstandard analysis open and closed monads to the left/right pierced and unpierced binads MoBiNad set infinitesimals infinities nonstandard reals standard reals nonstandard neutrosophic lattices of first type (as poset) and second type (as algebraic structure), nonstandard neutrosophic logic extended nonstandard neutrosophic logic nonstandard arithmetic operations nonstandard unit interval nonstandard neutrosophic infimum nonstandard neutrosophic supremum nonstandard analysis extended nonstandard analysis open and closed monads to the left/right pierced and unpierced binads MoBiNad set infinitesimals infinities nonstandard reals standard reals nonstandard neutrosophic lattices of first type (as poset) and second type (as algebraic structure), nonstandard neutrosophic logic extended nonstandard neutrosophic logic nonstandard arithmetic operations nonstandard unit interval nonstandard neutrosophic infimum nonstandard neutrosophic supremum


 0 kommentar(er)
0 kommentar(er)
